【爱化简的沈老师】专栏

沈鸣老师是青浦协和高中部的数学老师，他本科毕业于复旦大学数学系，并在香港城市大学获得博士学位。他在国际教育领域从事教育教学工作多年，拥有丰富的教学经验，最喜欢化繁为简，用最简单的语言，讲解最复杂的数学。

爱化简的沈老师，从现在开始将定期带领我们，从看似最简单的问题开始，引发和拓展我们对数学问题的深度思考，培养数学核心素养。

毕达哥拉斯定理 6B陈章涵,

为什么两个不同大小的圆，它们的周长直径比是相同的？

这个证明并不简单，需要用到极限，而极限属于高等数学里的概念。

除了需要用到极限，证明里还需要用一个定理：

相似三角形的对应边成比例。

这个定理，大多数同学都知道，但如果要求证明，大概跟“为什么两个不同大小的圆，它们的周长直径比是相同的”结果差不多。

相似三角形的对应边成比例，这个看似显然的结论，证明中需要的技巧性很高，还要用到一个非常重要的定理，勾股定理。

对于任意直角三角形，其斜边的平方和，等于两条直角边的平方和——这就是勾股定理。

用代数式表示勾股定理，就是

勾股定理，是中国传统的叫法，它在西方被称为毕达哥拉斯定理。

同一个定理，为何叫法不同？

我国西汉时期有本算书，名叫《周髀算经》，里面有记载，勾三股四弦五。

勾和股，是中国古代对直角三角形里，两条直角边的叫法。弦就是指斜边，也就是直角三角形里，最长的那条边。

勾三股四弦五，意思就是，一个直角三角形，两条直角边长度分别为3和4，那么斜边长度为5。

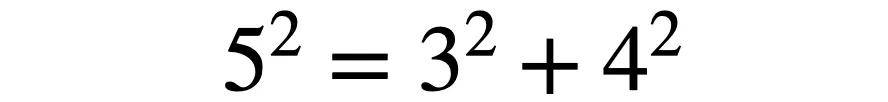
勾三股四弦五，虽然很正确，但遗憾的是，它算不上一个定理，最多只能算是符合定理的一个特例。

勾三股四弦五，勾五股十二弦十三，勾七股二十四弦二十五，这些都对，但都只是特例。

在数学的领域里，特例只是特例，再多的特例，未必是普遍规律，更不能构成定理。

毕达哥拉斯是古希腊的数学家，他发现这个规律的时间，比《周髀算经》晚了几百年。

然而，毕达哥拉斯给出了严格的证明，即对于任意直角三角形，其斜边长度的平方，都等于两条直角边的平方和。

证明非常简单，连小学生都能看懂。

给定一个边长为a+b的正方形ABCD，四条边上分别取四个点EFGH，分别把四条边分成a和b两部分。有两种方法，见下图。

第一种方法（见上图左边），连接EFGH，它刚好构成一个正方形。

因此，正方形ABCD的面积，等于正方形EFGH的面积，加上四个直角三角形的面积。

四个直角三角形，可以拼成两个长方形，长和宽分别为a和b。所以

第二种方法（见上图右边），正方形ABCD的面积，等于两个小正方形的面积，加上两个长方形的面积。

两个长方形，长和宽分别为a和b，还可以分成四个直角三角形。所以

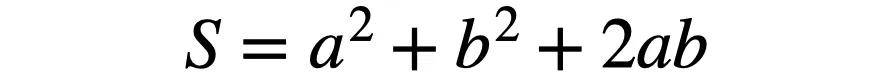
两种方式计算出来的结果相等，即

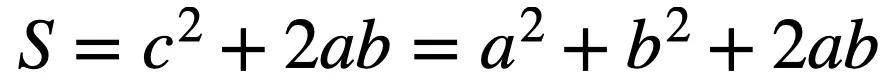
等号两边同时减去2ab，就可以得到

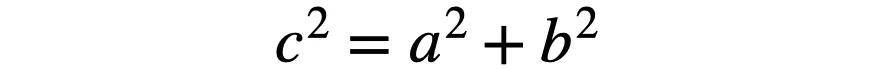
毕达哥拉斯给出的证明，奠定了这个关于直角三角形的重要规律，最终以他的名字来命名。

毕达哥拉斯定理，可谓名至实归。

毕达哥拉斯定理，可以说是最重要的几何定理，没有之一，因为很多几何定理的证明，都绕不开它。

比如上面提到的，想要证明两个不同大小的圆，它们的周长直径比是相同的，就要用到相似三角形的对应边成比例。而想要证明相似三角形的对应边成比例，就要用到毕达哥拉斯定理。

三角中的余弦定理，看起来跟毕达哥拉斯定理有点相似：

余弦定理，可视为毕达哥拉斯定理的推广。因为毕达哥拉斯定理，只适用于直角三角形，余弦定理可用于任意三角形，包括直角三角形。当角C是90度，它的余弦值为0，余弦定理的等式中，最后一项消失，刚好就是毕达哥拉斯定理。

毕达哥拉斯定理，可以说是余弦定理的一种特殊情况。

然而，余弦定理的证明，必须要用到毕达哥拉斯定理。

没有毕达哥拉斯定理，就没有余弦定理。

三角中还有一组重要的公式，名叫复合角公式：

复合角公式，是三角里所有关于角度公式的起点。无论诱导公式，倍角公式，还是辅助角公式，都可视为复合角公式的特例。

复合角公式的证明，需要用到余弦定理。而余弦定理的证明，绕不开毕达哥拉斯定理。

毕达哥拉斯定理，就好像几何大厦中，那块最底层的基石。

更神奇的是，通过毕达哥拉斯定理，可以推出无理数的存在。

一个直角三角形，两条直角边的长度都是1，使用毕达哥拉斯定理，可以计算得出，它的斜边长度等于根号2。

根号2，是一个无理数。

所谓无理数，不是无理取闹的数。

一个数，若可以表示成两个整数相除的形式，它就是有理数。

一个数，不是有理数，就是无理数。

利用反证法，不难证明，根号2无法表示成两个整数相除的形式，因此根号2不是有理数，而是无理数。

无理数有很多很多，比如根号2，根号3，根号5等，圆周率pi也是无理数。

事实上，有理数有无穷多个，而无理数比有理数还要多得多。

在毕达哥拉斯定理被发现前，人们并不知道无理数的存在，以为所有的数都是有理数。

作为一个几何定理，毕达哥拉斯定理还贡献了一个意外的副产品：数字中除了有理数，还有无理数。

事实上，有理数加上无理数，才构成了完整的数字大家族。

作为史上最伟大的数学家之一，毕达哥拉斯本可以通过无理数的发现，更上一层楼。

遗憾的是，毕达哥拉斯一直坚定地相信，所有的数，都可以表示为两个整数相除的形式，只有这样的数，才是完美的数。

信奉完美主义的他，无法接受任何不完美的数。

当他发现无理数的存在，认为这是一个漏洞，是对数字完美性的颠覆，他选择拒绝接受无理数，装作不知道。

更让人震惊的是，当毕达哥拉斯的学生希帕索斯，发现了根号2是无理数，去和毕达哥拉斯讨论。毕达哥拉斯为了隐瞒无理数的存在，竟然把希帕索斯扔进了海里……

追求极端的完美，结果极其不完美。

毕达哥拉斯定理，是一个伟大的发现，它让毕达哥拉斯名垂千史，也让他蒙上了污点。

完美的定理，在追求完美之人的手里，也会落得不完美。

完美的真理，经过不完美之人的诠释，也会变得不完美。

凡是大人物，尚有缺点、盲点。

作为普通人，更当慎之、鉴之。

常存谦卑的心，才能永攀真理大厦，更上一层楼。